Planar graphs

A plane graph is a graph drawn on the plane with curves representing edges and such that these curves do not intersect. A graph $G$ is said to be planar if it is isomorphic to a plane graph; such drawing is called a plane representation/plane drawing of $G$. There can be many ways to draw a given graph and some of them may not be a valid plane drawing.

See Figure 8 for two different ways to draw $K_4$ (a complete graph on four vertices).

Figure 8: Two drawings of $K_4$. Only one of them is a plane graph (valid plane drawing).

See in Figure 9 for some planar and non-planar graphs.

Figure 9: Drawings of planar (plane drawing) and non-planar graphs (no plane drawing).

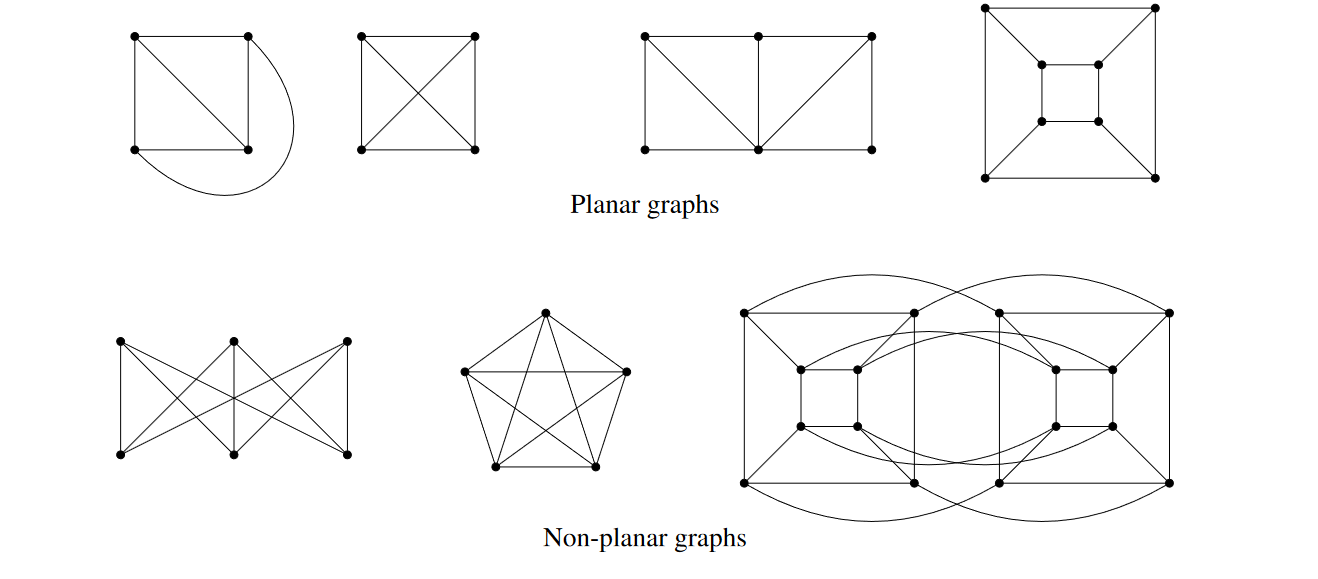
A drawing of a planar graph partitions the plane into regions (or faces)¹. Two points belong to the same region if they are connected via a curve that does not cross the drawing. For instance, the drawing of $K_4$ in Figure 8 has four regions. The students should be warned that it does not make sense to talk about regions of a planar graph. The notion of regions is associated with a specific plane drawing (plane graph), and the size and shape of a region depends on a specific drawing.

We start with a simple observation.

Lemma 6

Every plane drawing of a tree has exactly one region.

Proof:

This can be proved by induction on the number of vertices. When $n=1$, this is obvious. Assume that the statement holds for plane drawing off every tree of at most $n_0$ vertices. Now consider a plane drawing of a tree $G$ with $n_0+1$ vertices, and let $v$ be a leaf (from the Leaf lemma) so that $v'$ is the only neighbor of $v$. If we remove the curve corresponding to the edge $\{v,v'\}$ from the plane drawing of $G$, we obtain a plane drawing of $G-v$, applying the induction hypothesis on such drawing we learn that it has exactly one region. Now, adding the curve of $\{v,v'\}$ back into the plane does not have more than one region (this is because every curve that can be drawn to avoid crossing the drawing of $G-v$ can also be drawn to avoid crossing the drawing of $G$, by going ""around" the curve of $\{v,v'\}$ at vertex $v$)².

The following result sounds extremely intuitive but highly nontrivial to prove formally.

Theorem 7 (Jordan's Curve theorem)

Every plane representation of a cycle has exactly two regions (the interior and the exterior).

Theorem 8 (Euler's formula (1752))

For a connected plane graph $G$, we have that $|V(G)| + |R(G)| = |E(G)|+2$, where $R(G)$ is the set of regions in $G$.

Proof:

We prove this by induction on the value $|E(G)| - |V(G)|$. Since the graph is connected, we know that $|E(G)| -|V(G)| \geq -1$. The base case is when $|E(G)|= |V(G)|-1$ (a tree). In this case, we are done since $|V(G)|= |E(G)|-1$ and $|R(G)|=1$ (from Lemma 6. Now, assume that the induction hypothesis holds for every connected plane graph having $|E(G)| - |V(G)| = k \geq -1$. Our goal is to argue that IH holds for $|E(G)| - |V(G)| = k+1$. In this case, we know that the graph must have a cycle (from Theorem 6 and there exists an edge $e$ on this cycle that can be deleted while $G'=G-e$ remains connected. Applying the IH to $G'$, we know that Euler's formula holds. Moreover,

• $|V(G')| = |V(G)|$
• $|E(G')| = |E(G)|-1$
• $|R(G')| = |R(G)|-1$: Due to Jordan's curve theorem, edge $e$ is adjacent to exactly two distinct regions, and deleting it combines these two regions into one.

From this, we can deduce that the formula also holds for $G$.

A region is bounded by a number of edges (called sides of the region). It is possible that both sides of an edge are incident to the same region, and such edge would contribute twice to the number of sides of that region. See Figure 10.

Figure 10: A plane graph with the number of sides of each region.

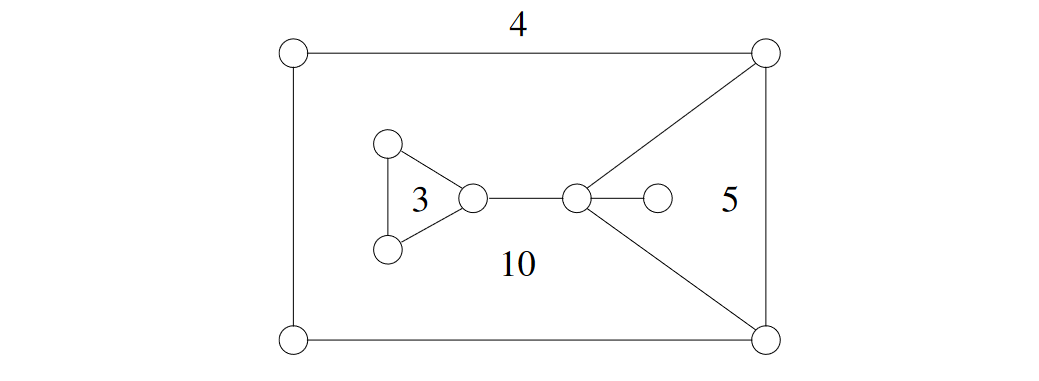
When a connected plane graph has at least three vertices, every region is bounded by at least three sides. Let $r_k$ denote the number of $k$-sided regions.

Lemma 7

In a connected plane graph with at least three vertices, $\sum_{k\geq 3} k\cdot r_k = 2m$.

Proof:

We use accounting method. Each edge pays two coins, one placed on each side. Each region collects the coins that are placed in its interior. Therefore, every $k$-sided region receives $k$ coins. We pay $2m$ coins in total. This implies the lemma.

Exercise 22

A planar graph with $n \geq 3$ vertices satisfies $m \leq 3n -6$ edges.

Hint: Use the previous lemma and Euler's formula.

This exercise implies a simple proof that $K_5$ is not a planar graph. To prove such a statement directly, one needs to argue that every plane representation must contain a crossing, which gets quite messy as one tries to write a proof (the students are encouraged to try this). However, let us see a super simple proof here: $K_5$ has five vertices and ten edges. Notice that, $10 \leq 3(5) -6$ is false, and therefore $K_5$ cannot be planar!

Theorem 9

Every planar graph is $6$-colorable (i.e. each vertex can be assigned a color so that neighboring vertices receive different colors, and the total number different of colors used is six).

Proof:

Since $m \leq 3n-6$, we know that there must be a vertex of degree at most $5$ (do you know why?). So we can create a coloring algorithm that picks the lowest degree vertex $v$, recursively colors $G-v$, and then greedily chooses the color of $v$ afterwards (since $v$ has at most five neighbors, there must be an unused color among the six available).

To prove the correctness of this algorithm formally, let us first consider a pseudocode (students should by now notice that pseudocodes that are suitable for proving correctness are relatively short and involve a small number of instructions).

$\mathrm{SixColor}(G)$

1. If $|V(G)| \leq 2$, assign different colors to different vertices
2. Let $v$ be a vertex with minimum degree (we know that $\deg(v) \leq 5$)
3. $\mathrm{SixColor}(G-v)$
4. Color $v$ using any color that is not used by $N(v)$ (the neighbors of $v$)

We prove the correctness of $\mathrm{SixColor}$ by induction on $n$. If $n\le2$, the coloring is trivially correct. Assume that the procedure is correct for planar graphs with at most $n_0$ vertices. When $|V(G)|= n_0+1$, we know that $G-v$ is colored correctly since $|V(G-v)| = n_0$ (by induction hypothesis). Since $v$ is colored differently from its neighbors, the whole coloring of $G$ is correct.

This is a baby step towards the celebrated Four Color Theorem: Every planar graph is $4$-colorable. As of today, the proof by Appel and Haken involves hundreds of cases. Coming up with an elegant proof would be a major breakthrough.

If a planar graph has more structure, these inequalities become stronger. In particular, we say that a graph is triangle-free if it has no subgraph isomorphic to $K_3$.

Exercise 23

Prove: A triangle-free planar graph with $n \geq 3$ vertices satisfies $m \leq 2n-4$ edges.

Exercise 24

Prove: Every triangle-free planar graph is $4$-colorable.

We end our discussions on planar graphs with an interesting characterization of planar graphs. As we have seen before, $K_5$ and $K_{3,3}$ are not planar. It turns out that these are more or less the only graphs that are not planar. To be more precise, we need a notion of homeomorphism. A subdivision of a graph is obtained by subdividing an edge by adding new vertices on the edge. For example, every cycle $C_k$ is a subdivision of $C_3$. Every path $P_k$ is a subdivision of an edge. Two graphs are homeomorphic if they are subdivisions of the same graph. Homeomorphic graphs have exactly the same drawings.

Theorem 10 (Kuratowski theorem)

A graph is planar if and only if it does not contain a subgraph homeomorphic to $K_5$ or $K_{3,3}$.

The above theorem is another remarkable characterization (in a similar spirit to the Eulerian characterization). It asserts the existence of "efficient certificates" about planarity in both directions. A planar graph can be certified by its plane representation (i.e., its drawing), and a non-planar graph can be certified by a $K_5$ or $K_{3,3}$ presence in the graph.

Footnotes

1. In most standard textbooks, the term face is preferred. In these notes, we will use the term region. ↩

2. A more formal argument would require more definitions. We hope this is convincing enough. ↩