Introduction

An (undirected) graph $G=(V,E)$ is a pair of vertex set $V$ and edge set $E$. Sometimes, we define only graph $G$ and use $V(G)$ and $E(G)$ to denote the set of vertices and edges respectively. An edge is an unordered pair of distinct vertices. Two vertices joined by an edge are said to be adjacent. A vertex $u$ and edge $\{u,v\}$ are said to be incident. Two vertices are neighbors if they are adjacent. The degree of vertex $v$, denoted by $\deg(v)$, is the number of its neighbors. A graph is regular if all vertices have the same degree. Unless stated otherwise, the number of vertices and edges will be denoted by $n$ and $m$ respectively.

Lemma 3 (Handshake)

$\sum_{v \in V} \deg(v) = 2m$

Proof:

We can prove this by induction on $m \geq 0$. If $m=0$, all vertices have degree $0$ and therefore the statement holds. Assume that this is true for $m=m_0$. To show that it is true for $m=m_0+1$, we remove edge $e=\{u,w\}$ from $G$ to get $G'$, so the graph $G'$ has $m_0$ edges. Applying the induction hypothesis, we have that $\sum_{v \in V} \deg_{G'}(v) = 2m_0$. Notice that the degrees of $G$ and $G'$ only differ at $u$ and $w$. In particular, $\sum_{v \in V} \deg_G(v) = \left(\sum_{v \in V} \deg_{G'}(v)\right) +2 = 2(m_0+1)$, implying what we want to prove.

Proving by induction is considered somewhat boring, although very systematic and tends to be free of mistakes. A more fun way to prove the above statement is by counting. Consider each vertex $v$ placing a coin on every incident edge. Notice that the total number of coins placed on the edges is $\sum_{v \in V} \deg(v)$. Each edge $e = \{u,w\}$ gets two coins placed on it, so the total number of coins is also equal to $2m$. This means that the two quantities are equal, implying the lemma. For the purpose of these lecture notes, we will call this accounting method¹.

Exercise 9

In this exercise, you are asked to write three different proofs of the following fact: In every graph, the number of odd-degree vertices is even.

1. Present a direct proof (hint: Use the Handshake's lemma)
2. Induction on $m$
3. Induction on $n$

This exercise will show that induction on different variables will not be equally hard.

The complement of $G$ is $\overline{G} = (V,\overline{E})$ where $\overline{E}$ is the complement with respect to the set of all pairs of vertices.

Observation 1

For any graph $G$, $|E(G)| + |E(\overline{G})| = {|V(G)| \choose 2}$.

A walk of length $k$ in $G$ is a sequence of vertices $v_0,v_1,\ldots, v_k \in V(G)$ such that $\{v_{i-1}, v_{i}\} \in E(G)$ for all $i=1,\ldots, k$. A path is a walk with no repeated vertices. A graph is said to be connected if there exists a path between every pair of vertices. A closed walk in a graph is a walk $(v_0,v_1,\ldots, v_k)$ with $v_0 = v_k$. A closed walk with no repeated vertices (other than $v_0 = v_k$) is called a cycle.

Next, we define the relation $\sim$ on the set $V(G)$ of vertices where $u \sim v$ if and only if there exists a walk from $u$ to $v$. It is easy to verify that $\sim$ is an equivalence relation².

Exercise 10

Prove that $\sim$ defines an equivalence relation.

This allows us to partition $V(G)$ into $V_1 \cup V_2 \cup \ldots \cup V_k$ based on the equivalence classes. Each subset $V_i$ is called a connected component. A graph is connected if and only if it has exactly one connected component.

The distance between $u$ and $v$ in $G$, denoted by $d_G(u,v)$, is the length of a shortest $u$-$v$ path in $G$.

Exercise 11

Prove that the distance function $d_G: V \times V \rightarrow {\mathbb R}_{\geq 0}$ is a metric. In particular, prove the following properties:

1. $d_G(u,v) = 0$ if and only if $u=v$.
2. (Symmetry:) $d_G(u,v) = d_G(v,u)$ for all $u,v \in V$
3. (Triangle inequality:) $d_G(u,v) + d_G(v,w) \geq d_G(u,w)$ for all $u,v,w \in V$

We now reach the first highlight of this chapter (which we will give two proofs for).

An Eulerian tour of $G$ is a closed walk containing all vertices and all edges, each edge exactly once (while vertices can be repeated). A graph possessing an Eulerian tour is said to be Eulerian.

Theorem 3 (Euler's Theorem (1736))

$G$ has Eulerian tour if and only if $G$ is connected and each vertex has even degree.

This kind of statement is called a characterization, that is, it asserts necessary and sufficient properties of Eulerian graphs. Mathematical characterization often implies "efficient certificates": An Eulerian graph can be certified by the existence of an Eulerian tour (and the validity of this certificate can be checked easily in linear time). Conversely, a non-Eulerian graph can be certified by a vertex with odd degree.

When we encounter an "if and only if" statement, we prove two implications. Notice that the direction $(\implies)$ is easy to prove. Therefore, our goal is to present two proofs for the converse.

First proof

The first proof is purely mathematical and does not directly yield an algorithm that finds an Eulerian tour (but it is possible to find one after some scrutiny). First, assume that $G$ is connected and each vertex has even degree. Take $T = (v_0,v_1,\ldots, v_{\ell})$ to be the longest possible walk in graph $G$ that does not repeat edges. We will argue that: (i) $v_0 =v_{\ell}$, and (ii) $E(T)= E$. This would imply that $T$ is an Eulerian tour.

To prove (i), assume for contradiction that $v_0 \neq v_{\ell}$. So $T$ must use an odd number of edges incident to $v_0$, and there must be an edge $e= \{v_0,w\}$ incident to $v_0$ that is not used in $T$. We can modify $T$ to start at $w$ and then follow exactly the same walk as $T$, obtaining a walk of length $\ell+1$ (that does not repeat edges), which contradicts the fact that $T$ is longest.

To prove (ii), we first argue that $V(T) = V$. Assume for contradiction that $w \not \in V(T)$. From connectedness of $G$, there is an edge $\{v_i, w'\}$ from some $v_i$ in $T$ and $w'$ not in $T$. We can again modify $T$ to start at $w'$ and follow exactly the same walk as a rotation of $T$ starting at $v_i$, a contradiction (here we need property (i); do you see why?). Next, we argue that $E(T) = E$. Assume otherwise that some edge $\{v_i, v_j\} \not \in E(T)$ (do you know why we can assume that the edge connects two vertices in the walk $T$?). We can modify $T$ to start at $v_i$ and follow exactly the same walk as a rotation of $T$ starting at $v_j$, obtaining again a contradiction.

Remark that the key here is to define $T$ to be the longest walk no repeating edges (the remaining arguments are straightforward). This trick is very useful in discrete mathematics and we encourage the students to try to digest the proof properly and keep this trick in mind for future use. The final remark before we proceed to the second proof: Do you see how an efficient algorithm follows from this? In particular, given a connected graph $G$ that has even degree, the algorithm should output an Eulerian tour of $G$.

Second proof

The second proof gives directly an efficient algorithm for finding an Eulerian tour in a graph. (It is in fact motivated by an algorithmic thinking). Let us try to start with the following simple subroutine that tries to find the longest walk no repeating edges greedily.

$\mathrm{GreedyTour}(G)$

1. $T \leftarrow (s)$ where $s$ is an arbitrary vertex.
2. while there is an unused edge that can extend $T$ do
   1. append the edge to $T$
3. return $T$

It is quite easy to check that $\textrm{GreedyTour}$ does not necessary return an Eulerian tour. But we can at least prove the following property (quite straightforward).

Exercise 12

$\textrm{GreedyTour}$ always returns a closed walk, i.e., the algorithm gets stuck at the same vertex it starts with. Recall that we are assuming $G$ to be connected an to have even degree.

Since $T$ is not necessarily optimal, what do we do? The idea is quite simple: Remove $T$ from $G$ and recurse on the remaining graph to find the tour $T'$ and ``stitch'' $T$ and $T'$ together to obtain the Eulerian tour. In particular, we look at the following algorithm.

$\mathrm{Euler}(G)$

1. $T \leftarrow \mathrm{GreedyTour}(G)$
2. Let $G_1,\ldots, G_{q}$ be the connected components obtained after deleting $E(T)$ from $G$.
3. return $\mathrm{Stitch}(T, \mathrm{Euler}(G_1), \ldots, \mathrm{Euler}(G_q))$

The algorithm makes use of the procedure $\mathrm{Stitch}(W_1,\ldots, W_{\ell})$ whose purpose is to combine several disjoint closed walks together into a single walk that visits each edge appearing in the walks exactly once. It is relatively straightforward to implement $\mathrm{Stitch}$.

Theorem 4

The algorithm $\mathrm{Euler}(G)$ returns an Eulerian tour of $G$.

Proof:

This can be proved by induction on the number of edges $m$. The base case when $m=0$ is trivial. Next, assume that the algorithm is correct up to input graphs with $m_0$ edges. Consider an input graph $G$ that has $m_0+1$ edges. Since each $G_i$ is connected and has even degree (why?), by the induction hypothesis, $\mathrm{Euler}(G_i)$ returns an Eulerian tour of $G_i$, which we call $T_i$. Finally, by the definition of $\mathrm{Stitch}(T, T_1,\ldots, T_q)$, we obtain a closed walk that visits every edge exactly once, hence an Eulerian tour. This concludes the proof.

Exercise 13

Draw the graphs in Figure 4 with a single line (i.e., you can neither lift your pen nor repeat the line (except while on a vertex) while drawing). Use arrows to indicate the direction of your drawing.

Figure 4: Graphs to be drawn in this exercise.

Exercise 14

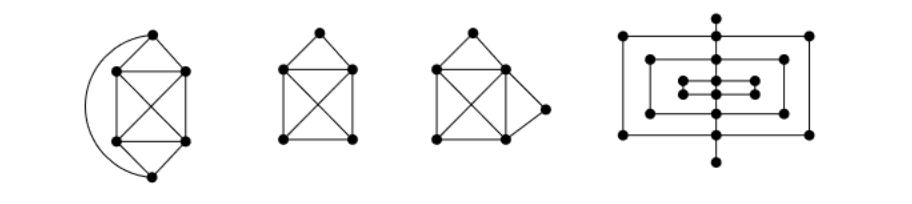
An Eulerian walk is a walk that visits all vertices and edges, each edge exactly once. Present a characterization of graphs that have an Eulerian walk but not an Eulerian tour. Prove that your characterization is correct.

Footnotes

1. This is the same as counting the number of persons. You can either count the number of heads, or the number of legs divided by two (assuming that everyone is alive, not decapitated, and nobody has lost their limbs...). ↩

2. A relation is called equivalence if it is reflexive ($(\forall v) v \sim v$), symmetric ($(\forall u,v)[u \sim v \Longleftrightarrow v \sim u]$) and transitive ($(\forall u,v,w)[u\sim v \& v \sim w \implies u \sim w]$). ↩