Isomorphisms

An important concept when working with graphs is called isomorphism. To motivate this concept, let us consider the following example.

Figure 5: Three graphs. The first is isomorphic to the second but non-isomorphic to the third.

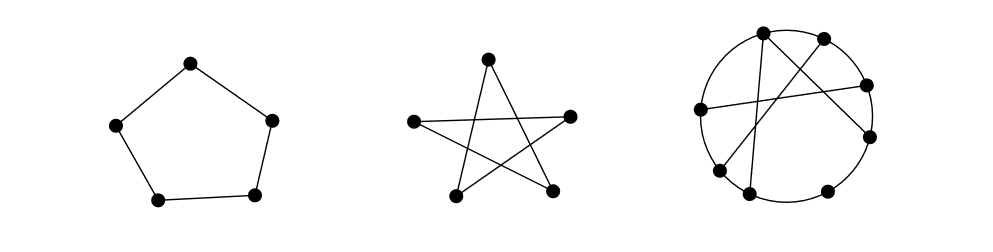
Although the first and second graphs look very different in drawing (the first is drawn so that edges cross as little as possible), a careful look would reveal that they are practically the same graph. Sometimes, two graphs may appear different in the names of vertices, but then their structures are the same. This "sameness" of structures is captured by the notion of isomorphism.

Two graphs $G$ and $G'$ are isomorphic if there exists a bijection $f: V(G) \rightarrow V(G')$ such that

$\{u,v\} \in E(G) \iff \{f(u), f(v)\} \in E(G')$

holds for every $u\neq v$. When $G$ and $G'$ are isomorphic, we write $G \cong G'$. We say that $f$ is an isomorphism between $G$ and $G'$.

Exercise 16

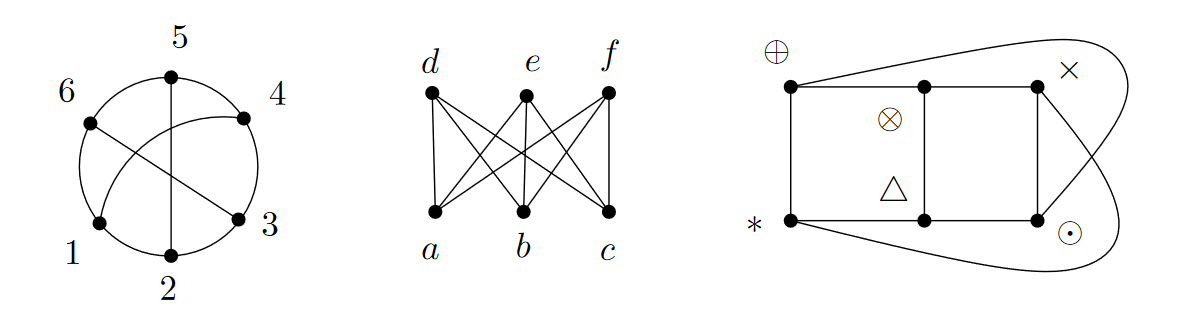
In Figure 6, three isomorphic graphs are shown. Define the appropriate bijections between them.

Figure 6: Three isomorphic graphs.

Exercise 17

Prove that $\cong$ defines an equivalence relation on the set of all $n$-vertex graphs.

An interesting question now arises. If we consider all $n$-vertex graphs, there are potentially $2^{{n \choose 2}}$ such graphs (each edge can either appear or be absent from a graph). How many "different" (non-isomorphic) graphs can there be? In particular, how many equivalence classes are there with respect to the relation $\cong$? For instance, when $n =3$, there are $8$ potential graphs but only $4$ non-isomorphic graphs.

Figure 7: All possible graphs on $3$ vertices.

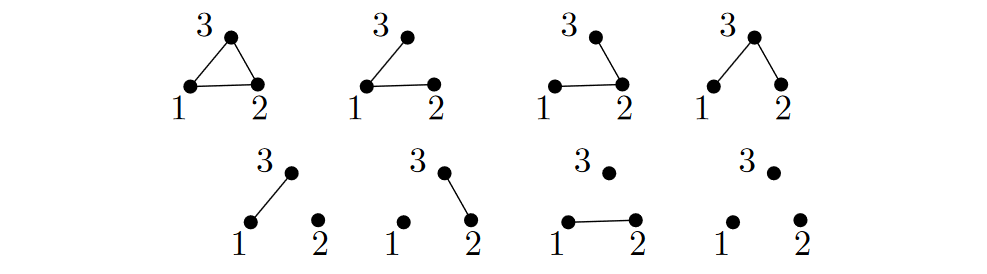
We will see that the number of $n$-vertex non-isomorphic graphs (denoted by $G(n)$) is not significantly less than $2^{{n \choose 2}}$.

Theorem 5

$2^{{n \choose 2}}/n! \leq G(n) \leq 2^{{n \choose 2}}$

Proof:

The upper bound was already discussed. To prove the lower bound, let ${\mathcal C}_1,\ldots, {\mathcal C}_{G(n)}$ be the equivalence classes of $\cong$. We use again the accounting method. For each $n$-vertex graph $G$, if $G$ belongs to ${\mathcal C}_i$, graph $G$ "pays a coin" to ${\mathcal C}_i$. The total number of coins paid in this process is exactly $2^{{n \choose 2}}$ (why?). Each ${\mathcal C}_i$ receives at most $n!$ coins (there are $n!$ bijections). Therefore, $G(n) \cdot n! \geq 2^{{n \choose 2}} \implies G(n) \geq \frac{2^{{n \choose 2}}}{n!}$

To see why this number is not much different from $2^{{n \choose 2}}$, let us compare their exponents.

$\log_2 2^{{n \choose 2}} = {n \choose 2} = \frac{n^2}{2}(1-1/n)$

As for the other number,

$\log_2 2^{{n \choose 2}}/n! = {n \choose 2} - \log_2 n! \geq {n \choose 2} - \log_2 n^n = \frac{n^2}{2}(1-1/n - 2 \log_2 n/n)$

When $n$ goes to infinite, both numbers are "roughly" $n^2/2$.

Exercise 18

An automorphism of $G$ is any isomorphism between $G$ and $G$ (itself), i.e., a bijection $f$ such that $\{u,v\} \in E$ if and only if $\{f(u), f(v)\} \in E$. A graph is called asymmetric if its only automorphism is the identity map. Prove that there are no asymmetric graphs with $4$ vertices.