Combinatorial estimates

In this section, we will learn a few tricks to prove inequality relations. The following inequality shows up a lot in analysis of algorithms and it is worth remembering.

Lemma 12 (Arithmetic-Geometric mean inequality (AM-GM))

For any two positive reals $a,b$, their geometric mean is no bigger than their arithmetic mean.

Proof:

We know that the square of any real number is non-negative, so let us try $0 \leq (\sqrt{a} - \sqrt{b})^2 = a + b - 2\sqrt{ab}$. Moving things around we get $(a+b)/2 \geq \sqrt{ab}$. The left-hand-side and right-hand-side are the arithmetic and geometric means respectively.

Exercise 75

For which pairs of positive reals $(a,b)$ do we have equality $\sqrt{ab} = (a+b)/2$? Justify your answer.

Exercise 76

Let $x_1,\ldots, x_n$ be positive reals. We will prove the following statement:

$AMGM(n): (\sum_{i=1}^n x_i)/n \geq (\prod_{i=1}^n x_i)^{1/n}$

Notice that we already proved the case when $n=2$. Here you will see an application of a rather weird mathematical induction.

1. Prove $AMGM(n) \implies AMGM(2n)$ for all $n\ge 2$.
2. Prove that $AMGM(n) \implies AMGM(n-1)$ for all $n\ge 4$.
3. Explain why the first and second parts together imply that the inequality holds for all $n$.

Exercise 77

The Harmonic Mean (HM) of two positive reals $a,b$ is defined by $2/(1/a+1/b)$. What is the relation between AM, GM, and HM? Prove your answer.

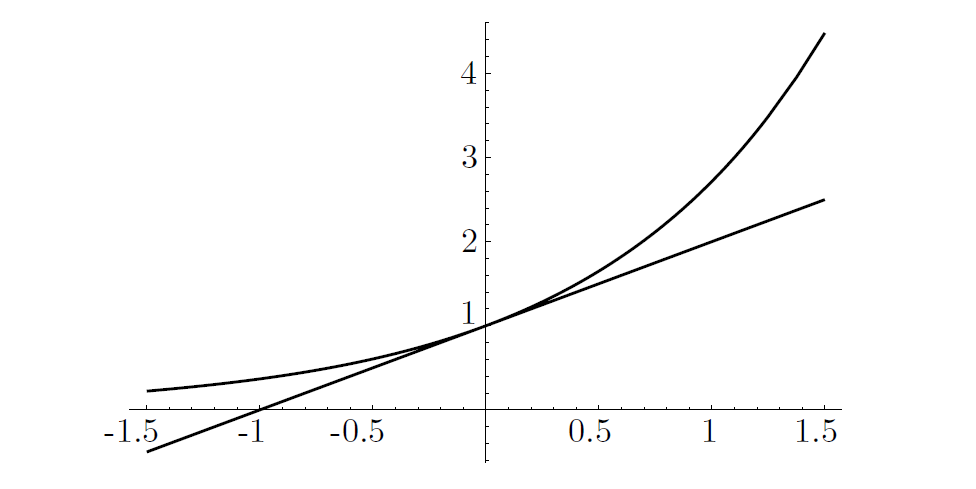
The following lemma is of extreme importance to computer scientists.¹

Lemma 13

Let $x$ be any real number. Then $1+x \leq e^x$.

We will not see a proof of this fact, but instead show a plot of both curves to convince ourselves. (Figure 14).

Figure 14: Comparison between two curves $y= 1+x$ and $y = e^x$.

Exercise 78 (Bernoulli's inequality)

Prove: For all $x \geq -1$ and $n \in {\mathbb N}$, we have $(1+x)^n \geq 1+nx$.

📄️ Factorial estimates

Let us start with a simple question:

📄️ Binomial coefficients

We give an estimate to the binomial coefficients. It is easy to see that ${n \choose k} \leq n^k$, but we can in fact prove a much stronger upper bound.

Footnotes

1. In the pre-tablet days, we would tell my students to cut out a piece of the lemma statement in paper and attach it to their bedroom's door. It is really super important ☺️ ↩