Application: Analyzing recursion

Counting can sometimes be used to analyze the running time of recursive algorithms. For instance, look at the following recursion. Let $d$ be some positive integer.

$T(n) = T(n-1) + T(n-d)$

and $T(1) = T(2) = \cdots = T(d) =1$. Intuitively, the program, when given an input of size $n$, calls two subroutines on smaller inputs (of sizes $n-1$ and $n-d$ respectively). Do you know how to prove a reasonable upper bound on the running time of this program?

For sure, we know that $T(n) \leq 2^n$ (we can use the fact that $T(n-d) \leq T(n-1)$ and then this becomes $T(n) \leq 2T(n-1)$ which solves to at most $2^{n}$). Can we do a better analysis?

Figure 13: Recursion tree.

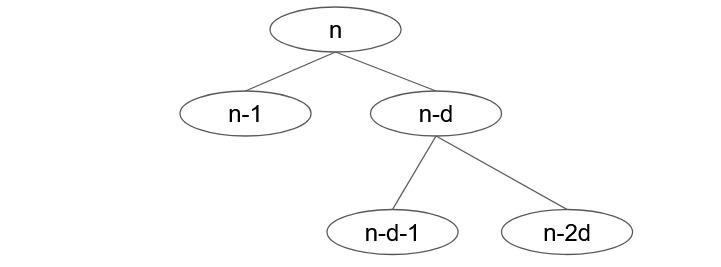
If we represent an execution of this algorithm as a recursion tree, it would look like Figure 13, where we would be interested in counting the number of leaves of this tree. In the tree, each node is labelled by the size of the instance and when a node with label $k$ is making recursive calls to sub-instances, this node would have two children of labels $k-1$ and $k-d$ respectively (as its left and right children).

To illustrate the idea of counting (in a somewhat sloppy but intuitive way), we can view each leaf $\ell$ as a sequence $s(\ell) \in \{L,R\}^*$, denoting the left or right turns that are taken from root towards it. Notice that $|s(\ell)| \leq n$. Moreover, the letter $R$ can appear in the sequence at most $n/d$ times (do you see why?). This implies that we have at most ${n \choose n/d}$ leaves. We will see later that this number is at most $2^{O((n \log d)/d)}$.

Exercise 74

Turn the previous sloppy proof into a real, formal proof 😊