Univariate polynomials

A polynomial of degree $n$ is a function of the form $f(x) = a_n x^n + a_{n-1}x^{n-1} + \ldots + a_1 x + a_0$ where $a_i \in {\mathbb R}$ for all $i$ and $a_n \neq 0$. Denote by $\deg(f)$ the degree of polynomial $f$. For example, $q(x) = x^3 + 2x^2 - 1$ is a polynomial of degree three with coefficients $a_3 = 1, a_2 = 2, a_1=0, a_0= -1$. The evaluation of $f$ at $a$ is $f(a)$. For instance, $q(2) = (2)^3 + 2 (2)^2 -1 = 15$. We say that $a$ is a root of polynomial $p$ if $p(a) = 0$.

Exercise 119

Prove: $f(x) \sim a_n x^n$ for every $x \ge 1$.

Below are two fundamental results that we rely on in this chapter. We will prove them later.

Theorem 43 (Roots of polynomials)

A non-zero polynomial of degree $d$ has at most $d$ roots.

Theorem 44 (Interpolation)

Given any $d+1$ points in the plane: $(x_1,y_1), \ldots, (x_{d+1},y_{d+1}) \in {\mathbb R}^2$ where the $x_i$'s are distinct, there exists a unique degree-$d$ polynomial $p$ with $p(x_i) = y_i$ for all $i \in [d+1]$.

The figures below show the cases for polynomials of degree $1$ and $2$.

Figure 15: The unique line (degree-1 polynomial) through $(1,2)$ and $(3,1)$.

Figure 16: The unique parabola (degree-2 polynomial) through $(-2,3)$, $(0,1)$, and $(4,10)$

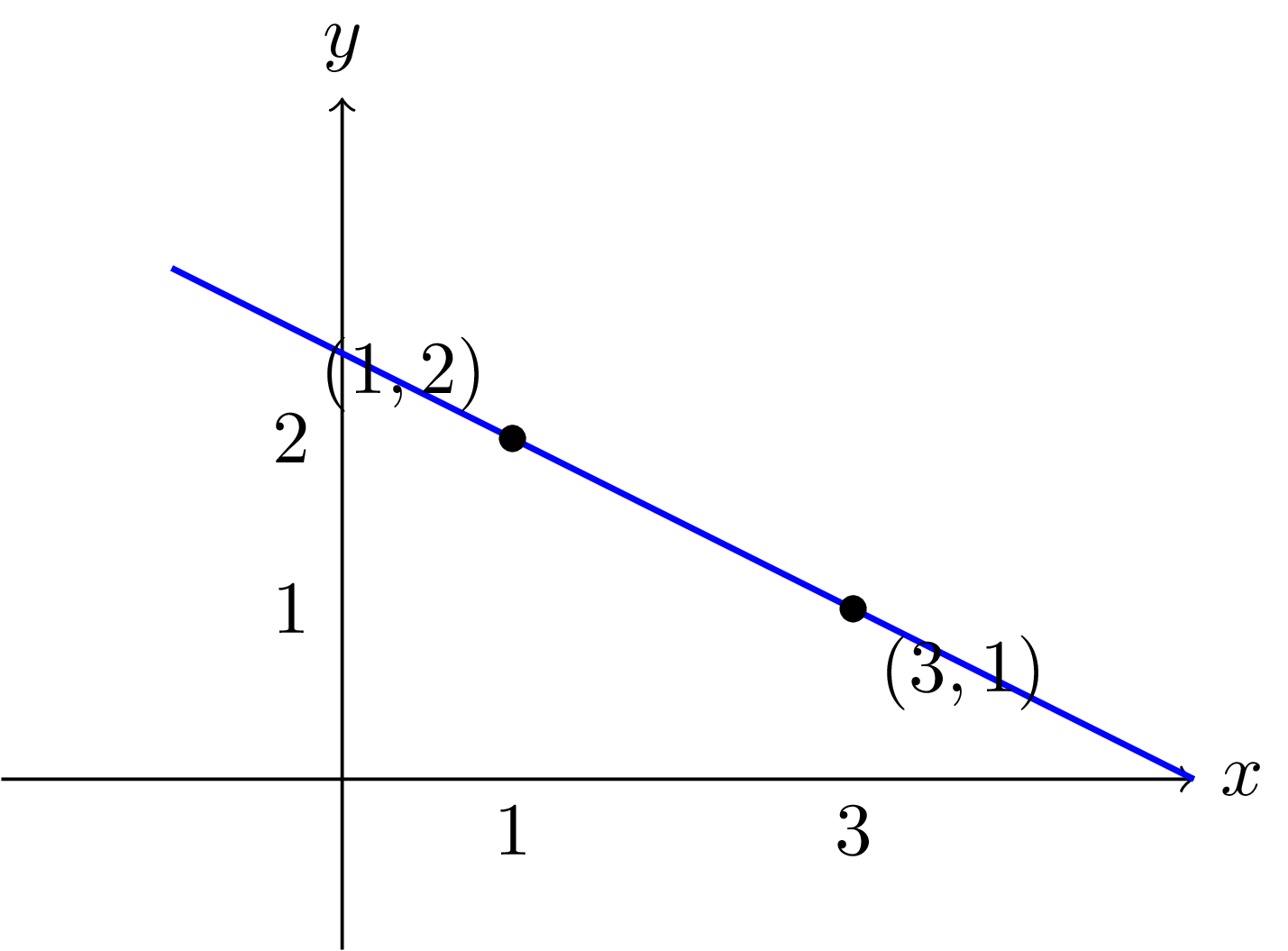
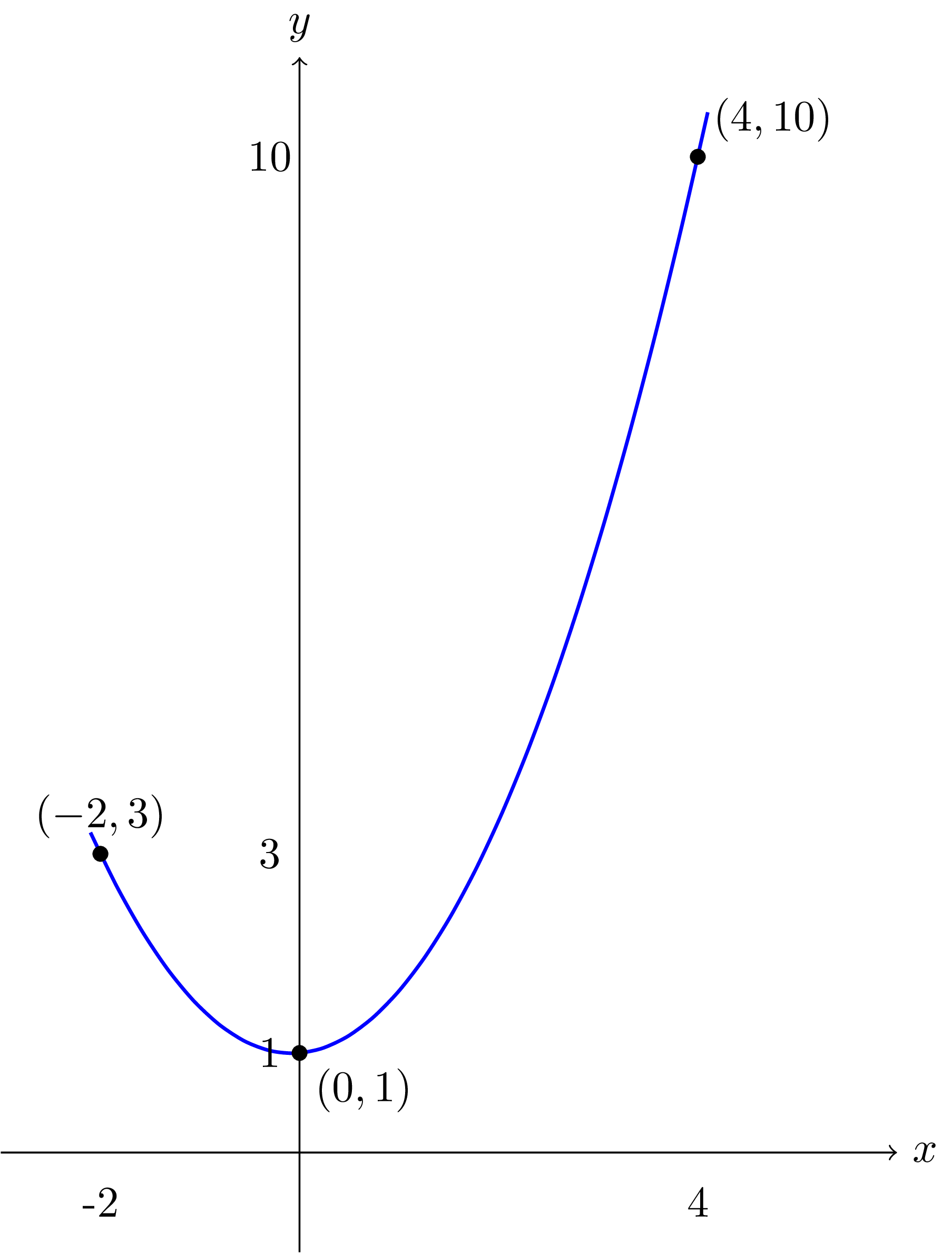
📄️ Proof of Theorem 44 (Interpolation)

We will assume Theorem 43 and prove Theorem 44.

📄️ Proof of Theorem 43 (Roots of polynomials)

We will need the following theorem which allows us to divide polynomials. This is an analogue of the integer division theorem that we saw in the number theory chapter.

📄️ Finite fields

Let us first warn everyone that, for those who have taken abstract algebra courses (groups, rings, fields), this section might be super boring 😊 This is our attempt to teach finite fields to (non-mathematician) computer scientists in an intuitive way without having to formally introduce groups, rings, and fields.

📄️ Application: Secret sharing

Four of us (Ariel, Amelia, Benjawan, Parinya) are working on the lecture notes for the course. Each person's mood is unpredictable and on a bad day one may decide to erase all the course documents.

📄️ Application: Error-correcting codes

A remarkable application of polynomials (and more generally, algebraic techniques in computer science) is in the construction of error-correcting codes.